The Z-score method

By Dr. Asoka Korale

The rather longstanding controversy concerning the Z-score method of translating raw marks into scores that determine university entrance is a matter that has surfaced once again and caught the public interest.

The university entrance for a faculty is based on the marks obtained with respect to several subjects. The distribution of marks with respect to each subject will vary depending on how each paper was received by the students that were examined in that subject.

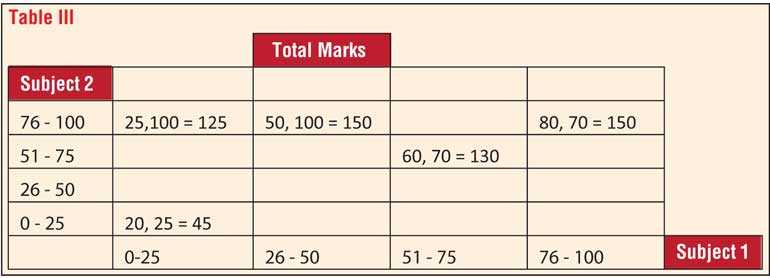
In the existing scheme each university and faculty determine a cut-off or score that reflects the effect of a combination of subjects under which each student has been examined in that year.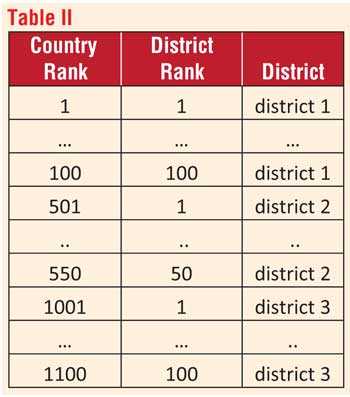  

Thus, it could be conceived as a scheme that allocates a score to each student depending on the rank achieved by that student in relation to peers that were examined in that subject. A combination of such scores from across the subjects is used to determine a final score and rank achieved in relation to the combination of subjects.

A rank is then simply one that measures the relative standing of a student in relation to peers that were examined under a subject. This final rank is then one that reflects the cumulative effect of the individual ranks achieved by a student in relation to peers in each subject.

Thus for example in a population of students that achieve marks of 40, 40, 70, 80 and 90, the marks could be adjusted to reflect a new set of marks with a new origin so that the translated marks are 0 ,0, 30, 40 and 50. In such a scenario relative scores of 0, 0, 30/50, 40/50 and 50/50 can be assigned for the raw marks of 40, 40, 70, 80 and 90.

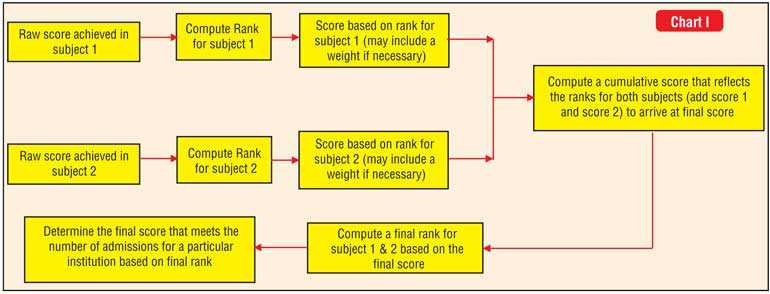
A scheme that reflects this idea is illustrated with an example in chart I.

Table I presents the scheme, considering two populations of marks obtained for two different subjects by 5 students. Each student is assigned a score for each subject that preserves the rank or relative standing in that subject in relation to peers. The scores achieved in relation to each subject is combined to obtain an overall score that reflects a student’s rank with respect to peers in each subject for the combination of subjects. This overall score is then ranked to determine how that student fairs in relation to peers in both subjects.

Additionally, a weight may be applied to each subject to scale the scores assigned for it in order to give emphasis over the other subjects if so desired.

A district-based system may also be considered where the student is ranked in relation to peers in that district in the same way to determine a district-based score of entry to a university. 

A simpler approach may also select students from a ranked list composed of the entire population so that each district meets its quota. Thus, the combined final scores and overall rank for a combination of subjects such as subject 1 and 2 is first computed for the entire country for a combination of subjects. And from this list, students are selected so that each district satisfies its quota, as illustrated in Table II.

This method does not assume a probability distribution from which the data is assumed to be drawn. It is also sensitive to outliers as result of normalising adjusted marks by the maximum rather than the mean. It assigns a score based on the range of marks obtained by the students in a subject. Since a certain fixed number of students are selected by a final rank obtained across several subjects, those that perform well would be highlighted and better performance in a one subject then offset weaker performance in another. 

Certain sports with multiple events are also scored in this manner where certain events count more than the others. This idea is representative of the skills that sportsmen possess where most do not excel in all areas but concentrate on events that would bring them most chance of victory and also those that count most towards a total winning score.

These characteristics are also representative of a student population where most do not excel in all subjects but possess different strengths and weaknesses in an individual ability to perform in relation to a group of peers. Those skills that are most likely to prove useful to succeed in an organisation or in an industry may also be concentrated in a few areas rather than a range of topics. In this view recognising individual ability in relation to specific areas may also prove worthy criteria in selecting candidates. 

In another approach the marks and score obtained by a student for a combination subjects may be considered separately for each subject. In a method termed cluster analysis several scores obtained with respect to different subjects may be analysed in relation to the data in Table III. 

This procedure is also equivalent to analysing the scores in relation to a probability distribution of two variables where each subject represents a probability distribution of arbitrary type. The distributions may be analysed independently or jointly depending on the dependence between the subjects.

In relation to table III different levels of performance in the two subjects may give similar aggregate results. The selection criteria may then consider both the aggregate as well as the individual marks. These marks may also be adjusted to reflect the maximum range in the scores.

The concept of outlier detection may also apply to the criteria of selection as appropriate where performance levels that are unusual may also be considered. In this view the student that scored 50 and 100 for subjects 1 and 2 for a total of 150 could be considered with the student that scored 80 and 70 for the same total. 

This idea is also related to how unusual a level of performance is compared to the rest of the student population. In this view many universities consider admissions on an individual basis accounting for numerous other criteria than on examinations alone.

The writer is a Chartered Engineer.